前言

自 Transformer 架构被提出以来，自注意力机制已成为处理序列数据，尤其是长程依赖建模的事实标准。其在自然语言处理领域的成功，也激发了其在计算机视觉领域的广泛应用。然而，将一个为离散、有序的文本数据设计的机制直接应用于连续、冗余的图像数据时，其固有的设计特性也带来了一些值得探讨的问题。

在写作《DCDN-DETR: A Dual-Stage Context Diffusion Network for Robust Small Object Detection》这一论文的过程中，从有效提取高级语义特征的角度出发，我设计了上下文引导的稀疏注意力(CGSA) 这一模块用于替换 Encoder 中原始的多头注意力。这一模块在高层次特征图上通过自注意力机制提取高级语义特征，并通过门控机制动态选择密集或稀疏的注意力通路。其中密集注意力(通过\text{Softmax})用于捕获全局关系，而稀疏注意力(通过\text{ReLU}^2)则通过非线性激活来削弱不相关的连接。两通路注意力经一个自引导的门控机制加权后得到最终的注意力图。尽管相比传统的多头注意力，CGSA 在 DCDN 的模型架构上得到了不错的结果，但一定仍然存在优化的空间。

受到我一个同学的毕业设计启发，我将目光投向了图卷积。与善于处理规则网格数据的卷积神经网络（CNN）不同，图卷积网络（GCN）专为处理不规则的图结构数据而设计。对于图中的任意一个节点，图卷积操作会聚合其所有直接相连的邻居节点的特征信息，然后结合该节点自身的原始特征，通过一个可学习的线性变换和非线性激活函数，来生成该节点在下一层的新特征表示。通过堆叠多层图卷积，一个节点能够感知到其多跳邻居的信息，从而学习到蕴含在图拓扑结构中的深层关系。这为超越传统 CNN 的网格限制和标准自注意力的全连接限制，提供了一种更灵活、更通用的关系建模框架。

标准自注意力机制在处理视觉任务时存在固有局限，而图卷积网络善于对结构化关系进行建模。这自然地引出一个问题：能否将图卷积的思想引入自注意力，以克服其瓶颈？本文将围绕这一思路展开，并尝试将 CGSA 与图结构结合，构建一个名为 G(raph)-CGSA 的融合架构。

自图论出发：从密集图到稀疏图

从图论的角度分析，标准自注意力机制可以被视为在一个全连接图上执行的特征聚合操作。输入序列中的每个 Token 都是图的一个节点，而注意力矩阵则定义了图中任意两个节点之间的连接权重。这种全连接的设计虽然保证了模型能够捕捉到全局任意位置的关系，但也付出了两方面的代价。第一是计算代价，即O(N^2)的计算和内存复杂度，这使得模型难以扩展到高分辨率图像等长序列任务。第二是信息代价，即信噪比损失。在多数视觉任务中，图像的大部分区域通常是低信息密度的背景。自注意力在全局\text{Softmax}归一化时，必须将总为 1 的注意力权重分配给所有 Token。这也就意味着，空间上占主导地位的背景区域会不可避免地分走一部分注意力权重，从而稀释了分配给那些面积小但信息量大的关键目标区域的权重，造成了一种语义污染。

为了缓解上述问题，一些研究致力于对注意力矩阵进行稀疏化。这些方法通常在计算出密集的注意力矩阵之后，通过引入额外的机制（如特定的激活函数或 Top-K 选择）来过滤掉弱连接。这可以看作是一种被动过滤的思路，其前提仍是：需要生成一张完整的、包含大量冗余信息的密集图。

既然最终目的是稀疏化，那么可不可以转守为攻，去主动构建一张稀疏图？以特征图的区域为节点，区域间的语义相似性为边，似乎可以构建出图结构。

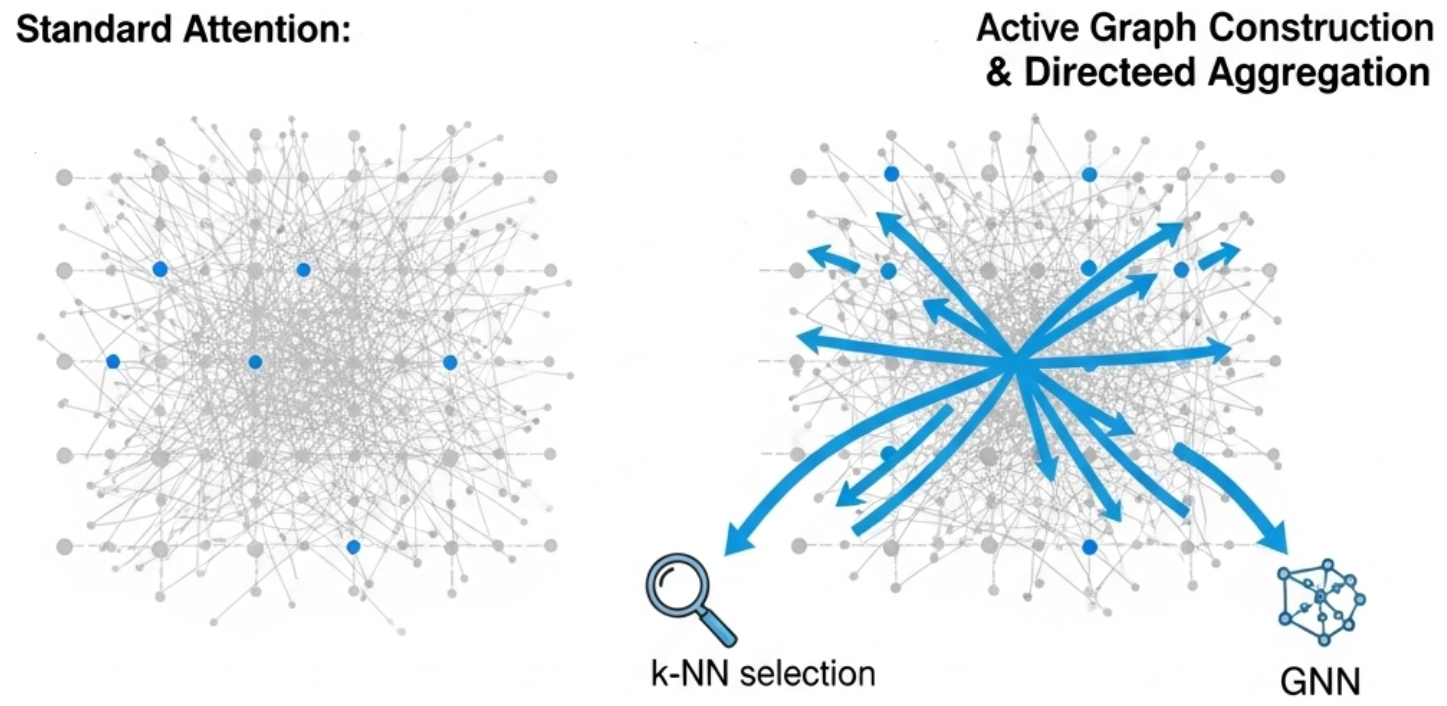
于是我尝试去设计 G-CGSA 模块。视觉元素之间的有效关联本身就是稀疏的，因此一个更优的架构应该在进行信息聚合之前，就先识别出这张内在的稀疏图。它不再试图从一个充满噪声的池子里打捞信号，而是直接构建一个只包含高价值信号的纯净信道。这一从后处理过滤到前置构建的转变，是 G-CGSA 设计的初步思路。

G-CGSA 的初步构建思路

首先，将输入的特征图X \in R^{C \times H \times W}中的每个空间位置的特征向量视为一个图节点，将问题域从传统的序列处理转向图处理。随后，它通过两步操作：图构建与信息聚合来完成对上下文的提纯。

第一步是主动图构建。此阶段的目标是建立一个只包含强语义关联的稀疏连接图。G-CGSA 采用 k-近邻（k-NN）算法，并以余弦相似度（即两个向量的夹角的余弦值）作为节点间语义相关性的度量标准。对于图中的任意节点i，其特征为f_i，需要计算它与所有其他节点j的特征f_j的余弦相似度S_{ij}：

之后，选取值最高的 k 个节点作为其邻居集合\mathcal{N}(i)。这一步完成后，节点间的连接关系便从全连接收缩为稀疏的 k-NN 连接。

第二步是定向信息聚合。在构建好的稀疏图上，使用图注意力网络（GAT）来聚合信息。GAT 允许模型为每个邻居学习一个独立的注意力权重\alpha_{ij}，从而实现有差别的加权聚合。\alpha_{ij}通过在邻居集合\mathcal{N}(i)内进行\text{Softmax}归一化得到：

其中，a代表一个可学习的函数，\mathbf{W}代表可学习的权重矩阵。然后，使用计算出的注意力权重\alpha_{ij}对邻居节点变换后的特征进行加权求和，从而更新节点i的特征表示f'_i：

其中，\sigma代表非线性激活函数，\alpha_{ij} = \text{Softmax}_j(a(\mathbf{W}f_i, \mathbf{W}f_j))。

通过这个流程，G-CGSA 将一个全局且高开销的注意力计算，重构为一个在稀疏结构上的、高效的局部信息交换过程。再将这个注意力模块置于外部 FFN中，即构建出了一个新的 Encoder。

import torch
import torch.nn.functional as F

# GATLayer 是一个图注意力网络层
# X (Tensor): 输入的Token特征，形状为 (N, C)，N为Token数量，C为特征维度 
# k (int): k-近邻算法中的邻居数量

def GCGSA(X: Tensor, k: int) -> Tensor: # (N, C)
    N, C = X.shape
    nodes = X
    # 1.主动图构建
    nodes_norm = F.normalize(nodes, p=2, dim=1)
    sim_matrix = torch.matmul(nodes_norm, nodes_norm.t())
    sim_matrix.fill_diagonal_(-float('inf'))
    # 找到每个节点的k个最近邻
    _, topk_indices = torch.topk(sim_matrix, k=k, dim=1)
    # 构建图的边索引
    row = torch.arange(N).view(-1, 1).repeat(1, k).view(-1)
    col = topk_indices.view(-1)
    edge_index = torch.stack([row, col], dim=0)
    # 2.定向信息聚合
    gat_layer = GATLayer(in_features=C, out_features=C)
    updated_nodes = gat_layer(nodes, edge_index)
    return updated_nodes

可能的局限性：敏感性、精度-速度权衡与长距关联语义的损失

由于目前没有时间做实验，仅从目前的理论来看，G-CGSA 似乎有几点局限性，欢迎一起探讨。

首先是超参数 k​ (k 近邻邻居数量)的敏感性与固定性。不同图像的场景复杂度千差万别，同一图像的不同区域所需要的上下文范围也可能不同。对于一个内容简单的区域，较小的 k​ 值就足够了，过大的 k​ 反而可能引入噪声；而对于一个内容复杂的区域，则可能需要更大的 k​ 值来捕捉充分的上下文。采用固定的 k​ 值缺乏灵活性，如何让模型根据输入动态地、自适应地调整 k​ 值，是后续可以具体思考的内容。

另外，图构建阶段的计算开销也不容忽视。尽管 G-CGSA 避免了自注意力计算的O(N^2)复杂度，但图构建阶段的朴素 k-NN 算法需要计算一个 的相似度矩阵，其本身的开销也是O(N^2)。虽然可以采用近似最近邻（ANN）搜索等方法来加速这一过程，但这又会引入近似误差，可能影响最终性能，同时也增加了实现的复杂性。因此，在构图效率和构图精度之间存在一个需要权衡的 Trade-off。

最大的局限在于，G-CGSA 损失了部分真正的全局信息通路。标准自注意力的核心优势在于其能够一步到位地连接序列中的任意两个 Token。而 G-CGSA 通过 k-NN 建立的连接，本质上是在特征空间中的局部连接。也就是说，一个节点无法直接与那些和它特征不相似、但在空间上或语义逻辑上却至关重要的远距离节点进行通信。例如，在一张描述十字路口的图片内，一个远处的红绿灯节点，其特征可能与近处的汽车节点差异很大，但它却是该场景中的关键上下文。G-CGSA 的图构建机制可能会剪掉这条重要的长程异构连接，而标准自注意力则有可能捕捉到它。

结语

通过引入显式的由数据驱动的图结构，将注意力机制从一个密集的全局广播，转变为一个稀疏、高效的结构化通信方式。这种转变在处理含有大量冗余信息的视觉数据时，在理论上显示出了一些优势。

G-CGSA 的初步设计做出了一种权衡：用特征空间中的局部连接，换取了对噪声的有效抑制和在计算上的专注性。也许进一步地，可以探索可学习的、动态的图结构；例如，模型能否根据输入内容自适应地决定邻居的数量 k，甚至直接学习边的存在与否，而非依赖固定的 k-NN 规则？或者，可以设计混合模型，将 GCSA 中稀疏图的精准性与标准注意力的全局性结合起来。 这可能是一个并行的双通路架构，或是一种允许少许的长距离关键连接被添加到稀疏图中的机制，以弥补其在捕捉某些长距离、异构信息上的潜在损失（这又要考虑到如何判断何种长距离连接为关键连接）。

将图神经网络的结构化推理能力与 Transformer 的强大序列建模能力融合起来，应用于视觉领域应当是一个不错的方向。

这篇 Blog 在这里作为一个 Note，记录一下昨天灵光一现的想法。提醒我等明年有时间的时候，再对这个方向进行进一步的探索。